La structure de la matière solide

2.      La structure de la matière solide :

Grâce aux forces de liaison les atomes se regroupent et se placent dans leurs positions d’équilibre pour former des corps solides; comment s’organisent- ils ?

Lorsque les atomes sont chimiquement liés les uns aux autres, il y aura des distances interatomiques d’équilibre qui sont déterminées par la condition que l’énergie totale doit être minimale. Donc dans un solide constitué de plusieurs atomes du même type, l’état d’équilibre est seulement obtenu lorsque tous les atomes posséderont le même environnement. Ceci conduit à un arrangement périodique tridimensionnel des atomes. Cette formation se fait suivant une configuration ordonnée, à trois dimensions, dans laquelle les atomes sont régulièrement répartis. Ainsi est défini un « réseau spatial »; les atomes constituent les « nœuds » du réseau. La même chose est vraie pour les solides constitués de plus d’un type d’atomes ; dans ce cas des unités composées de plusieurs atomes sont périodiquement réputées.

L’état contraire de l’état solide cristallin est l’état amorphe. Dans un solide amorphe il n’existe pas un ordre à grande distance, cependant, un ordre à courtes distances peut être détecté.  

3.1. Définitions :

Le cristal idéal ou parfait (le cristal réel diffère mais peu) est constitue d’une répartition régulière des atomes, des ions ou des molécules suivant les trois dimensions de l’espace et l’arrangement régulier des atomes s’étend pratiquement à l’ infini.

Un cristal peut être décrit a l’aide d’une entité mathématique, le réseau, et d’un contenu matériel, lemotif. « L’assemblage » constitue le cristal (figure 6).

Un réseau cristallin est décrit par une entité mathématique de base appelée réseau. Ce n’est pas un cristal. C’est un ensemble de points qui n’a aucune matérialité.

Le réseau est défini par l’ensemble des points M qui peuvent être décrit par le vecteurdonné par :n1 + n2 avec n1,2=0, ±1, ±2, ±3, ±4,… (Figure 7a), ceux-ci formant les nœuds du réseau, occupés ou non par des atomes. La localisation des nœuds est déterminée par un système vectoriel (  et ) dans le réseau plan. Chaque point du réseau cristallin peut être généralement représenté par le vecteur

La Maille = tout polyèdre ayant pour sommets des nœuds du réseau, et tel que l’empilement de polyèdres tous identiques au premier puisse remplir tout l’espace sans vide ni recouvrements de matière.

Les vecteurs de base, qui sont en général quelconques, forment un repère oblique. Pour un réseau donné, le choix des vecteurs de base et donc de la maille, n’est pas univoque. Ce fait est illustré par la figure 7b qui correspond à un réseau plan.

Une rangée réticulaire est définie par une droite passant par minimum deux nœuds. p est appelé paramètre de la rangée réticulaire et correspond à la distance entre deux nœuds de la rangée réticulaire (figure 7a).

Une maille est dite primitive ou simple si elle ne possède des nœuds que sur les sommets du parallélogramme (réseau plan) ou du prisme (réseau à trois dimensions) correspondant (figure 8). Par d’autres mots, Une maille primitive est la plus petite entité qui permette de générer l’ensemble des nœuds par des translations entières de réseau.

Dans un réseau plan, l’aire de toutes les mailles primitives est identique. De même pour un réseau tridimensionnel, le volume d’une maille simple est un invariant qui correspond au volume offert à chaque nœud. S’il existe des nœuds supplémentaires (à l’intérieur, sur les faces ou les arêtes), la maille est dite multiple.

Pour compter le nombre de nœuds contenus dans une maille élémentaire, il faut tenir compte du fait que les sommets du polyèdre appartiennent simultanément a un nombre p de mailles adjacentes ; chacun d’eux comptera donc pour 1 /p nœud. Il est possible de démontrer qu’une maille élémentaire contient toujours un nombre entier N de nœuds.

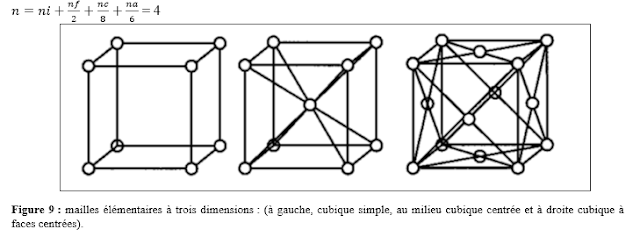
Pour illustrer comment on compte le nombre de nœuds dans une maille donnée, on utilise la figure 9 qui représente plusieurs types des mailles cubiques.

ni le nombre de nœuds à l’intérieure de la maille, nf le nombre de mailles sur les faces (chaque nœud est partagé entre deux mailles), nc le nombre de maille aux coins ( chaque nœud est partagé entre huit mailles) et na le nombre des nœuds aux centres des arêtes, (chaque nœud compte pour ¼). Par exemple, le nombre de nœuds par unité de maille de la structure cubique à face centrées (ni = 0, nf=6, nc=8 etna=0) (figure 10(c)) est :